ASYMPTOTIQUES (CALCULS)

ASYMPTOTIQUES (CALCULS)

Il est difficile de définir avec précision ce que l’on appelle méthodes asymptotiques en analyse mathématique. Ainsi, lors de l’étude d’une suite ou d’une fonction dont la nature est compliquée, certaines questions ne nécessitent que des renseignements d’ordre qualitatif tels que f (x )0 ou f (x )+ 秊 pour x+ 秊. D’autres exigent un contrôle quantitatif très précis, défini par des inégalités explicites. Les comportements asymptotiques relèvent d’une préoccupation intermédiaire: dans de nombreux problèmes, on remplace la quantité étudiée par une autre plus simple sans que, «à la limite», le résultat soit modifié. Par exemple, la relation

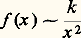suffit à établir la convergence à l’infini de l’intégrale de f . Les exemples qui suivent montreront la nature de ces préoccupations.

Du point de vue strictement technique, les méthodes asymptotiques sont extrêmement variées et, en dehors de quelques résultats relativement généraux, chaque cas particulier exerce l’ingéniosité de celui qui l’étudie. Nous nous limiterons, dans les chapitres 2 et 3, à l’exposé de quelques-unes de ces méthodes.

1. Comparaison de la croissance des fonctions

L’étude de la manière dont des quantités tendent vers l’infini ou tendent vers zéro a constitué, à la naissance du calcul infinitésimal, au XVII^e siècle, la théorie des «infiniment grands» et de leurs inverses, les «infiniment petits», et a fait l’objet de polémiques passionnées, souvent paramathématiques (cf. histoire du CALCUL NUMÉRIQUE). En effet, l’absence d’une conception précise de la notion de limite (problème qui ne fut pas abordé sous forme rigoureuse) rendait mystérieuse la nature de ces quantités qui, tout en étant comparables entre elles, n’étaient pas comparables aux nombres ou aux fonctions. De plus, cela représentait l’intrusion de l’infini dans les calculs et, bien que cet infini fût potentiel et non actuel (en ce sens que l’infini n’était pas considéré en lui-même comme un être mathématique soumis à des règles opératoires précises), cela suscitait des problèmes philosophiques aux mathématiciens, échaudés par les nombreux «paradoxes de l’infini» qui n’étaient pas encore clairement analysés. La recherche des «vraies valeurs» des formes indéterminées, rencontrées dans le calcul des dérivées par exemple, allait cependant montrer l’importance de ces notions et les justifier, tout au moins empiriquement, aux yeux des mathématiciens. Ces questions ont été systématiquement élucidées par Paul Du Bois-Reymond, qui, dans une série d’articles de 1870-1871, a posé les fondements du calcul des infiniment grands (Infinitär-calcul ) en mettant en évidence l’importance de la notion d’échelle de comparaison; il a étudié également en détail l’intégration et la dérivation des relations de comparaison. Tous ces résultats ont trouvé leur forme rigoureuse et définitive dans les travaux de Hardy.

Relations de comparaison

Dans de nombreuses questions d’analyse, on est conduit à étudier l’«ordre de grandeur» d’une fonction f (n ) d’une variable entière positive pour n grand, ou d’une fonction f (x ) d’une variable continue x lorsque x est grand, ou voisin d’une valeur a . Formulons le problème de manière précise, en nous limitant au cas d’une variable continue pour fixer les idées.

Soit f une fonction, à valeurs réelles ou complexes, définie pour a 漣 h 麗 x 麗 a ou a 麗 x 麗 a + h (on dira alors que f est définie dans un voisinage à gauche ou à droite de a ) ou pour x assez grand (on dira que f est définie au voisinage de l’infini). Par exemple, l’application:

transforme les voisinages à droite de a en les voisinages de l’infini et, par suite, on peut, en considérant la fonction:

ramener l’étude de f au voisinage de a (à droite) à l’étude d’une autre fonction au voisinage de l’infini; nous nous limiterons à ce cas dans ce chapitre. Il est clair, d’autre part, que les notions ci-dessous s’étendent de manière évidente au cas où la variable ne prend que des valeurs entières. Nous nous proposons ici de montrer qu’il est possible de «comparer» les fonctions définies au voisinage de l’infini lorsque la variable tend vers l’infini.

Si f et g sont deux fonctions définies pour x assez grand et à valeurs non nulles, on dit que f et g sont asymptotiquement équivalentes pour x tendant vers l’infini, et on note:

au voisinage de l’infini si le rapport f (x )/g (x ) tend vers 1 pour x tendant vers l’infini. Remarquons que cela n’entraîne même pas que la différence f (x ) 漣 g (x ) soit bornée, comme le montre l’exemple des fonctions asymptotiquement équivalentes x ² + x et x ² au voisinage de l’infini. La recherche de fonctions équivalentes à des fonctions données et plus simples ou plus maniables est un problème essentiel (cf. Partie principale , in chap. 2) et qui peut être fort difficile; ainsi, si 神(x ) désigne le nombre de nombres premiers 諒 x , la «loi de répartition des nombres premiers», conjecturée par Gauss, qui exprime que: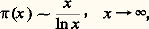

est un résultat profond de la théorie des nombres, qui n’a été démontré qu’en 1896 par Hadamard et de La Vallée-Poussin (cf. théorie des NOMBRES – Théorie analytique).

Nous allons maintenant préciser comment on peut comparer les croissances des fonctions pour x秊. On dit que f est asymptotiquement négligeable devant g , ou que g croît plus vite que f pour x tendant vers l’infini, si pour tout 﨎 礪 0, on a |f (x )| 諒 﨎 |g (x )| pour x assez grand; on écrit alors:

Il est clair que la définition ci-dessus signifie que le rapport f (x )/g (x ), s’il est défini pour x assez grand, tend vers 0. Remarquons que le symbole de Landau doit être considéré seulement comme une écriture commode mais ne représente pas une fonction déterminée croissant moins vite que g et ne doit donc pas être manipulé comme les nombres ou les fonctions; ainsi écrire que o(g ) + o(g ) = o(g ) exprime que la somme de deux fonctions négligeables devant g est négligeable devant g , mais cela n’aurait aucun sens d’en conclure que o(g ) = 0! Pour une formulation mathématique satisfaisante, on pourrait convenir que o(g ) désigne l’ensemble des fonctions négligeables devant g , qui est un espace vectoriel; la notation f = o(g ) est alors un abus de langage pour f 捻 o(g ).

La notation précédente permet de traduire maintenant facilement les résultats sur la «croissance comparée» des fonctions puissance, logarithme et exponentielle; ainsi, pour a 麗 b ,

pour a quelconque et b 礪 0, on a:

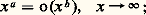
c’est-à-dire les fonctions puissance croissent plus vite que les fonctions logarithme. Enfin, pour a quelconque, c 礪 0 et d 礪 0,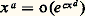

au voisinage de l’infini, c’est-à-dire les fonctions exponentielles croissent plus vite que les fonctions puissance.

Indiquons, pour terminer, une dernière notation fort utile. Dans de nombreux cas, on a besoin d’une relation de comparaison plus faible que la précédente, qui puisse s’appliquer à des fonctions dont la croissance n’est pas très régulière. S’il existe une constante M telle que |f (x )| 諒 M |g (x )| pour x assez grand, on dit que f est dominée par g pour x tendant vers l’infini, et on écrit:

bien entendu, si f est négligeable devant g , elle est aussi dominée par g . Si g est la fonction constante 1, l’égalité f (x ) = O(1) exprime simplement que f est bornée pour x assez grand; par exemple: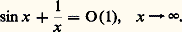

Le symbole O permet de préciser certains ordres de croissance; ainsi écrire que:

est plus précis que: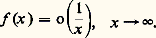

Les Anglo-Saxons utilisent les notations de Hardy: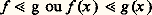

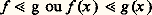pour f est négligeable devant g , ou:

pour f est dominée par g .

Fonctions de comparaison et échelles de comparaison

Les fonctions les plus simples auxquelles on est tenté de comparer (au sens du chapitre 1) une fonction donnée, pour x tendant vers l’infini, sont les fonctions:

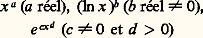et les produits d’un nombre fini de telles fonctions. Remarquons au passage que, à l’exception de la fonction 1 (obtenue pour a = 0), chacune de ces fonctions tend vers 0 ou vers l’infini lorsque x tend vers l’infini; de plus, d’après les propriétés de croissance comparée de ces fonctions, si f et g sont de ce type, on a une et une seule des trois relations:

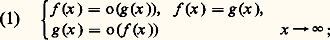cette propriété signifie que deux fonctions distinctes f et g du type considéré ont des croissances que l’on peut comparer et ne font pas «double emploi», en ce sens qu’il n’existe pas de constante c telle que f (x ) 黎 cg (x ), x秊. De manière générale, une famille E de fonctions définies et positives pour x assez grand peut être utilisée de manière profitable pour étudier la croissance d’une fonction quelconque si, quelles que soient f et g dans E, on a une et une seule des relations (1); on dit alors que la famille E constitue une échelle de comparaison pour x tendant vers l’infini. Bien entendu, toute partie d’une échelle de comparaison en est aussi une; dans la pratique, on se limite à des échelles logarithmico-exponentielles constituées de fonctions du type considéré ci-dessus ou de composées (au sens de la composition des fonctions) de telles fonctions, par exemple:

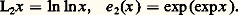On utilise souvent des échelles de comparaison dénombrables; l’exemple le plus simple est:

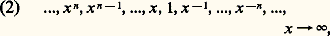qui est décroissante , en ce sens que chaque terme est négligeable, pour x tendant vers l’infini, devant tous les termes précédents. Indiquons, pour terminer, que le choix d’une échelle de comparaison dépend essentiellement du type de fonction que l’on veut étudier et il serait illusoire d’espérer trouver une échelle dénombrable telle que toute fonction s’«intercale» exactement dans l’échelle; en effet, on peut montrer que, pour toute échelle dénombrable, il existe une fonction qui croît plus vite que toute fonction de l’échelle (Du Bois-Reymond) et une fonction qui croît moins vite que toute fonction de l’échelle (Hadamard).

Tout ce qui précède sur les relations de comparaison au voisinage de l’infini se définit de même pour les fonctions définies dans un voisinage (à droite par exemple) d’un point a : ainsi l’échelle de comparaison qui correspond à (2) est dans ce cas:

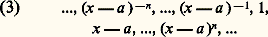2. Développements asymptotiques

Dans ce chapitre, on supposera choisie une échelle de comparaison E (au voisinage d’un point a ou au voisinage de l’infini).

Partie principale

L’idée la plus simple pour étudier le comportement d’une fonction donnée f (au voisinage de a ou de l’infini) est de chercher si, à une constante près, elle est équivalente à une fonction de l’échelle E choisie. S’il existe une telle fonction g de E et une constante c 0 telles que f 黎 cg , c et g sont déterminées de manière unique et on dit que cg est la partie principale de f (par rapport à l’échelle E); remarquons que cela équivaut à dire que:

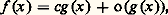ou encore que f (x )/g (x ) tend vers une limite finie c 0. Dans le cas où l’échelle choisie est (2) ou (3), on retrouve la notion usuelle de partie principale; ainsi, 1/sinx a pour partie principale 1/x pour x0, e ^x 漣 e ^a a pour partie principale e ^a (x 漣 a ) pour xa ,

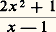a pour partie principale 2x pour x秊. Remarquons que la partie principale n’existe pas nécessairement; en effet, toutes les fonctions d’une échelle logarithmico-exponentielle sont positives pour x assez grand et par suite une fonction «oscillante» (comme x sinx , qui s’annule dans tout voisinage de l’infini) n’est comparable à aucune fonction de ce type, pour x秊. Il se peut aussi que l’échelle choisie ne soit pas assez «riche» et que f croisse plus vite ou moins vite que toute fonction de l’échelle, ou encore tombe dans un «trou» de l’échelle: ainsi la fonction x ln x n’a pas de partie principale par rapport à l’échelle (2), car elle croît plus vite que x et moins vite que x ².

Développements asymptotiques au sens de Poincaré

Si f a une partie principale c ¹g ¹ par rapport à une échelle E, on peut chercher à préciser un peu plus le comportement de f en étudiant la différence f 漣 c ¹g ¹; si cette fonction a une partie principale c ²g ², on a alors:

De manière générale, on appelle développement asymptotique (au sens de Henri Poincaré) d’ordre k d’une fonction f par rapport à une échelle de comparaison E une somme finie (nécessairement déterminée de manière unique si elle existe):

telle que la différence f 漣 g soit négligeable devant g ^k (cf. chap. 1); ainsi:

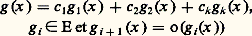
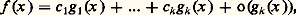les g ⁱ formant une suite «décroissante» de fonctions de E, en ce sens que, pour chaque i , la fonction g ^{i + 1} est négligeable devant g ⁱ .

L’exemple le plus simple de cette situation est la théorie classique des développements limités au voisinage d’un point a : ce n’est autre que la recherche du développement asymptotique d’une fonction par rapport à l’échelle (3). Le résultat classique le plus important est ici la formule de Taylor , qui affirme que toute fonction k fois continûment dérivable au voisinage de a admet le développement limité d’ordre k :

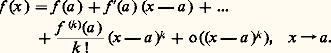On obtient ainsi, pour les fonctions usuelles de l’analyse, des développements limités d’ordre arbitrairement grand; par exemple, au voisinage de 0:

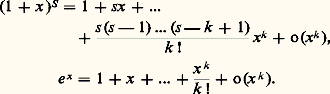On trouvera de nombreux autres exemples dans l’article SÉRIES.

Les résultats précédents permettent déjà d’étudier un grand nombre de formes indéterminées.

3. Cas des intégrales

Il s’agit d’étudier le comportement asymptotique des restes des intégrales convergentes:

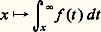ou d’évaluer des intégrales divergentes:

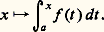Cette étude s’effectue en deux étapes. On se ramène au cas où f appartient à une échelle classique de comparaison, grâce au théorème d’intégration des relations de comparaison:

Théorème . Si f et g sont positives et équivalentes au voisinage de + 秊, alors:

– dans le cas convergent:

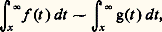– dans le cas divergent:

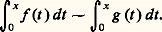Les énoncés sont analogues pour les relations f = o (g ) et f = O (g ). En revanche, on ne peut pas toujours dériver les relations de comparaison; par exemple:

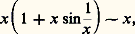mais:

n’est pas équivalent à 1.

Pour f appartenant à une échelle classique, si on ne dispose pas d’une primitive explicite, on effectue des intégrations par parties successives. Par exemple, le comportement asymptotique du logarithme intégral: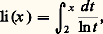

étudié par Euler et Gauss, est donné par:

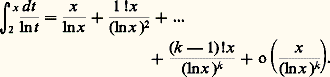De même, la fonction d’erreur, introduite par Gauss en calcul des probabilités,

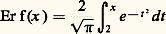tend vers 1 si x+ 秊 et son développement asymptotique se déduit de la relation:

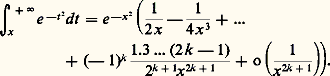Il est important de ne pas confondre les développements asymptotiques avec les séries; dans de nombreux cas, on n’est capable de déterminer explicitement qu’un petit nombre de termes et d’obtenir cependant ainsi de très précieux renseignements sur les fonctions considérées. De toute façon, un développement asymptotique est essentiellement une somme finie et, même si on peut obtenir un nombre arbitrairement grand de termes, cela n’entraîne nullement que la série correspondante converge, comme le montre l’exemple suivant, étudié par Laplace. Considérons la fonction:

(à une constante près, c’est la fonction «exponentielle-intégrale»); par intégration successive par parties, on obtient facilement, pour tout k ,

on constate facilement que, pour tout t , la série de terme général (k 漣 1)!/t ^k est divergente.

Dans l’exemple du logarithme intégral li (x ) donné ci-dessus, on remarquera même que tous les termes du développement tendent vers + 秊 avec x !

À travers les exemples précédents, on voit que le rôle de l’intégration par parties est de transformer l’intégrale à étudier en une intégrale négligeable devant la précédente. On peut expliquer le schéma de calcul de la manière suivante. Soit l’intégrale: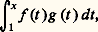

où f varie lentement devant g (par exemple f (t ) = 1/t , ou f (t ) = ln t , et g (t ) = e ^t , g (t ) = exp (face=F0019 漣 t ²), ou g (t ) = e ^it ). En première approximation, on assimile f à une constante, ce qui conduit à l’estimation:

où: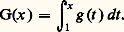

La non-constance de f se traduit par l’apparition d’un terme correctif portant sur la dérivée de f , ce qui constitue la formule d’intégration par parties:

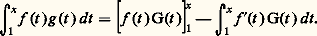La faible variation de f se traduit par le fait que l’intégrale du second membre est négligeable devant l’intégrale initiale. Dans les applications, on rencontre très souvent le cas de l’amortissement constant g (t ) = e ^-kt ou de la phase tournante uniforme g (t ) = e ⁱ size=1^{諸 t} . Ce double aspect amortissement et phase tournante se retrouve dans la méthode de Laplace et dans la méthode de la phase stationnaire (cf. chap. 5).

4. Cas des séries

Généralités

Le cas du développement asymptotique des sommes partielles des séries est analogue à celui des intégrales. Il s’agit d’étudier le comportement asymptotique des restes de séries convergentes:

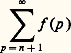et des sommes partielles de séries divergentes:

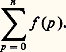Ici encore, on se ramène au cas où f appartient à une échelle classique, grâce au théorème de sommation des relations de comparaison:

Théorème . Si f et g sont positives et équivalentes au voisinage de + 秊, alors:

– dans le cas convergent:

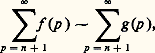– dans le cas divergent:

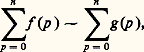Enfin, lorsque f appartient à une échelle classique, on compare les sommes précédentes à des intégrales. Cette comparaison est facile lorsque f varie «lentement»; plus précisément, on a:

Théorème de Hardy . Soit f une fonction à valeurs complexes de classe 暈¹, pour x 閭 0, telle que sa dérivée f soit intégrable au voisinage de + 秊. Alors, la suite:

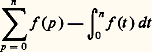est convergente.

Par exemple, la suite:

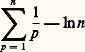admet une limite, traditionnellement notée 塚 et appelée constante d’Euler. Ce nombre est de nature encore très mystérieuse et on ne sait même pas s’il est rationnel ou irrationnel. Une valeur approchée à 20 décimales est:

Formule sommatoire d’Euler-Maclaurin

Si l’on désire un développement asymptotique à une précision plus grande, on fait appel à une technique beaucoup plus élaborée, la formule sommatoire d’Euler-Maclaurin. On suppose ici que f est suffisamment dérivable et que, pour tout entier k , la dérivée k -ième f ^(k) est négligeable devant f ^(k-1) .

On se propose d’évaluer des sommes du type: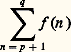

par comparaison avec l’intégrale:

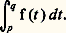Plus précisément écrivons:

on se ramène d’abord à l’intervalle [0, 1] pour chacune des intégrales de la somme de droite par les changements de variable u + n 漣 1 = t . On a, pour chacune de ces intégrales: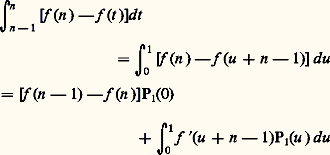

après intégration par parties, en prenant une primitive P¹ du polynôme constant P⁰ = 1. De même, en prenant une primitive P² de P¹, on a, par intégration par parties:

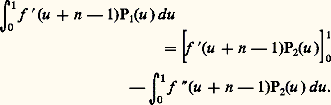On poursuit ce processus jusqu’au rang r , c’est-à-dire jusqu’à un reste portant sur f ^(r+1) , et on choisit les primitives successives P^k de P⁰= 1 de telle sorte que les termes tout intégrés disparaissent deux à deux dans la sommation lorsque n varie de p + 1 à q . Il suffit pour cela d’imposer au polynôme P^k de vérifier les relations: P ^k = P^k-1 pour k 閭 1 et P^k (1) = P^k (0) pour k 閭 2, ou, ce qui revient au même, pour tout k 閭 1,

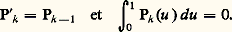On démontre qu’il existe une suite (P^k ) et une seule satisfaisant à ces conditions. Plus précisément, pour tout entier naturel k ,

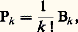où B^k est le k -ième polynôme de Bernoulli, considéré par J. Bernoulli comme solution de l’équation aux différences: P(x + 1) 漣 P(x ) = kx ^k-1 . Ces polynômes peuvent être introduits par la série génératrice formelle:

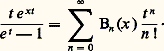En fait, dans ce qui précède, seuls interviennent les nombres de Bernoulli 廓^k = B^k (0). Pour les valeurs de ces nombres, on se reportera à l’article histoire du CALCUL NUMÉRIQUE.

Pour expliciter les calculs précédents, il convient de distinguer deux cas, suivant que:

f est intégrable au voisinage de + 秊; il s’agit alors d’évaluer le reste:

f n’est pas intégrable; il s’agit alors d’évaluer la somme partielle: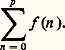

Ces deux cas sont explicités dans l’article sur l’histoire du calcul numérique déjà cité, avec des exemples classiques, comme la formule de Stirling et des applications à la fonction gamma.

Il convient de noter que la formule sommatoire d’Euler-Maclaurin est de type asymptotique, c’est-à-dire que les restes ne tendent pas nécessairement vers 0. Mais, lorsque ce reste tend vers 0, la formule sommatoire fournit des développements en série. Ainsi, appliquant cette formule à la fonction t 料 e ^zt , on montre que, pour |z | 麗 2 神,

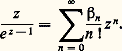On en déduit les développements en séries entières des fonctions trigonométriques:

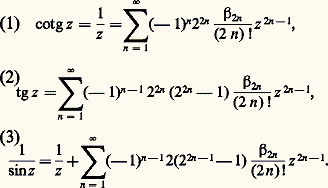La formule d’Euler-Maclaurin s’applique à l’évaluation de sommes portant sur une fonction f dont les dérivées décroissent de plus en plus. Les cas les plus fréquents en mathématiques appliquées sont ceux où f présente un amortissement constant, une phase tournante constante, et la situation mixte. Par exemple, supposons que l’on veuille évaluer:

avec z = x + iy , x 閭 0 (z 2ik 神) et 見 閭 0. On peut penser à comparer e ^-nz /n size=1^見 à l’intégrale: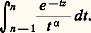

Or, en première approximation, 1/t size=1^見 varie peu sur [n 漣 1, n ] tandis que e ^-tz présente de manière mixte un amortissement et une phase tournante, ce qui conduit à l’estimation:

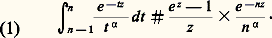Autrement dit, le terme e ^-nz /n size=1^見 est multiplié par un facteur constant dû à l’amortissement et à la phase. L’estimation précédente permet de conjecturer:

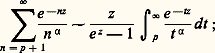pour établir rigoureusement cette relation, il faut évidemment remplacer l’estimation (1) par une intégration par parties comme indiqué supra .

5. Cas des fonctions définies par des intégrales

Nous dégagerons ici trois méthodes importantes pour étudier le comportement asymptotique d’intégrales dépendant d’un paramètre lorsque ce paramètre tend vers l’infini.

La méthode de Laplace

Considérons une fonction:

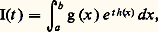définie par une intégrale; (a, b ) est ici un intervalle quelconque, borné ou pas. Pour simplifier, nous supposerons que la fonction h admet un seul maximum. L’idée essentielle ici est que, sous cette hypothèse, c’est la partie de l’intégrale située au voisinage de ce maximum qui est prédominante pour t grand; par suite, si on remplace la fonction g (x ) e ^th(x) par sa partie principale au voisinage de ce point, il est plausible que l’on obtienne, par intégration, la partie principale de I(t ) pour t tendant vers l’infini. Nous nous limiterons à un cas particulier simple où le raisonnement ci-dessus est applicable. Plus précisément:

Théorème 1 . Soit g et h deux fonctions continûment dérivables dans un intervalle [a , b [ borné ou pas (on suppose cependant a fini) telles que g (x ) e ^th(x) soit intégrable sur [a , b [ pour t assez grand. Supposons de plus que la fonction h admet un maximum pour x = a tel que h (a ) = 0, h (a ) 麗 0, et g (a ) = 0 et que le maximum de h (x ) dans tout sous-intervalle [a , b [, avec a 礪 a , est inférieur à h (a ); on a alors:

Par exemple, si:

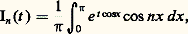on obtient:

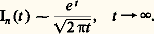Donnons également une application à la fontion gamma d’Euler (cf. fonction GAMMA):

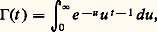qui extrapole la factorielle, à savoir, pour n entier naturel, 臨(n + 1) = n !. Après changement de variable u = xt , on obtient:

où l’intégrale est la forme ci-dessus avec h (x ) = lnx 漣 x . La fonction h admet un unique maximum pour x = 1 dans l’intervalle (0, + 秊) et h (1) = 漣 1; appliquant le théorème 2 à chacun des intervalles (0, 1) et (1, + 秊), ce qui revient à multiplier par 2 la formule du théorème 1, on obtient la célèbre formule de Stirling: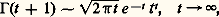

qui précise le comportement asymptotique de la fonction gamma lorsque t tend vers l’infini. Le développement asymptotique de ln 臨 peut être obtenu par la formule d’Euler-Maclaurin (cf. histoire du CALCUL NUMÉRIQUE).

La méthode de la phase stationnaire

La méthode de la phase stationnaire a été utilisée par lord Kelvin en 1887, à propos de problèmes d’hydrodynamique, pour étudier des intégrales du type:

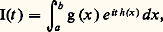où g et h sont des fonctions très régulières dans (a , b ); dans les applications physiques, g (x ) apparaît comme l’amplitude et th (x ) comme la phase du phénomène considéré. L’idée essentielle de Stokes et Kelvin est que la partie prédominante de l’intégrale pour t tendant vers l’infini est obtenue au voisinage des extrémités de l’intervalle d’intégration et surtout au voisinage des points c où la phase est «stationnaire», c’est-à-dire tels que h (c ) = 0. Intuitivement, lorsque t est grand, le point g (x ) e ^ith(x) tourne «très vite» autour de 0 dans le plan complexe au voisinage de tout point c de l’intervalle (a , b ) tel que h (c ) 0, et cela a pour conséquence de rendre «petite» la partie correspondante de l’intégrale; si maintenant h (c ) = 0, la phase est stationnaire au voisinage de c , c’est-à-dire que cette rotation est très ralentie et la contribution de l’intégrale au voisinage d’un tel point est prédominante sur le reste. Ce principe peut présenter de nombreux aspects; nous nous limiterons, à titre indicatif, à deux énoncés mettant en évidence le rôle joué par les extrémités de l’intervalle d’intégration, d’une part, et par la présence de points où la phase est stationnaire, d’autre part. En fait, c’est la contribution de ces derniers qui est prépondérante sur la contribution des extrémités.

Théorème 2 (rôle des extrémités de l’intervalle d’intégration). Soit g et h deux fonctions indéfiniment dérivables dans l’intervalle compact [a , b ]. Si la fonction h n’a pas de point stationnaire dans l’intervalle, on a:

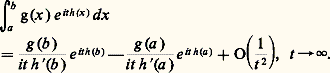Théorème 3 (rôle des points où la phase est stationnaire). Supposant encore que g et h sont indéfiniment dérivables dans l’intervalle compact [a , b ], nous supposerons, de plus, que h s’annule en un seul point c de cet intervalle avec g (c ) 0 et h (c ) 0. Alors on a, pour t tendant vers l’infini:

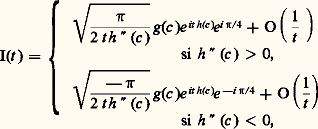Nous renvoyons aux ouvrages spécialisés pour l’étude détaillée des cas obtenus par superposition des phénomènes ci-dessus et pour le cas des intervalles non compacts.

La méthode du col

Cette méthode a été utilisée par Riemann en 1863 pour étudier le comportement asymptotique de la fonction hypergéométrique et Debye l’a systématiquement développée dans deux mémoires de 1909 et 1910. Il s’agit d’étudier, pour t réel tendant vers l’infini, des intégrales du type:

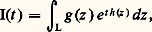où L est un chemin, fini ou pas (pouvant dépendre de t ), contenu dans un ouvert D du plan complexe dans lequel g et h sont des fonction analytiques. Le théorème de Cauchy montre qu’on peut, dans de nombreux cas, modifier le chemin L sans changer la valeur de l’intégrale; la méthode du col consiste à profiter de cette possibilité en choisissant un chemin L sur lequel la fonction w (z ) = |e ^th(z) | = e ^tReh(z) n’atteigne son maximum qu’en un seul point, dans des conditions qui permettent d’appliquer la méthode de Laplace (un peu modifiée pour tenir compte du fait que h prend des valeurs complexes). Intuitivement, on choisira le chemin L passant par un point z ⁰ de telle sorte que, sur L au voisinage de ce point, la phase Im h (z ) varie peu, alors que l’amplitude w (z ) décroît assez vite. Indiquons l’aspect géométrique de cette question, ce qui justifiera la terminologie utilisée. Considérons dans l’espace à trois dimensions la surface d’équation z = w (x + iy ) = e ^tReh(x+iy) , appelé le relief de e ^th(z) . Cette surface ne présente pas de «sommet» relatif, d’après le principe du maximum pour les fonctions analytiques, et, par suite, les seuls points où le plan tangent est horizontal (ce sont les points où la dérivée h (z ) s’annule), sont des cols; on dira donc qu’un point z ⁰ du plan complexe tel que h (z ⁰) = 0 est un col ; l’ordre du col est, par définition, le nombre m tel que:

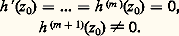Revenons à l’interprétation géométrique; les lignes de niveaux du relief (c’est-à-dire les courbes w = C ^te ) ont pour projection sur le plan des z = x + iy , les courbes sur lesquelles Reth (z ) reste constant; les lignes de plus grande pente du relief, qui sont orthogonales aux lignes de niveau, ont pour projection les courbes du plan complexe sur lesquelles la partie imaginaire de th (z ) reste constant. Le long d’une telle courbe, e ^th(z) a une phase constante, alors que son module varie «le plus vite possible», car les lignes de plus grande pente sont les lignes de gradient du relief. Limitons-nous, pour simplifier, au cas d’un col d’ordre 2. Par un tel point passent deux lignes de niveau et deux lignes de plus grande pente, la ligne de faîte, qui suit la crête, et la ligne de thalweg, qui descend dans la vallée. L’idée, ici, est essentiellement de chercher une ligne L qui passe par un seul col et qui soit aussi proche que possible (au voisinage de ce col) de la projection de la ligne de thalweg; en effet, sur cette dernière, la phase de e ^th(z) reste constante et le module de e ^th(z) présente un maximum au col. Si on sait trouver une telle ligne, la méthode du col consiste à remplacer l’intégrale étudiée par l’intégrale prise le long d’un petit segment de la tangente à la ligne de thalweg du col, et de remplacer g et h par leurs développements aymptotiques dans cette intégrale.

Donnons un exemple significatif de cette méthode. Dans ce qui suit, nous considérerons seulement des chemins infinis L:

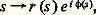définis pour 漣 秊 麗 s 麗 + 秊, et satisfaisant aux conditions (A):

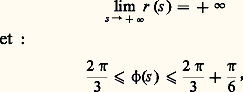au voisinage de + 秊;

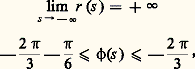au voisinage de 漣 秊 (cf. figure).

On voit facilement, en appliquant le théorème de Cauchy et en passant à la limite, que l’intégrale d’Airy, introduite en 1838 par Airy dans ses recherches sur l’optique:

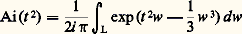ne dépend pas du chemin L, pourvu qu’il satisfasse aux conditions (A). Effectuant le changement de variable: w = tz , on a:

où le chemin L¹ = t ^-1L satisfait encore (A); appliquons la méthode du col à cette intégrale. La fonction h (z ) = z 漣 z ³/3 a pour dérivée h (z ) = 1 漣 z ², d’où deux cols + 1 et z ⁰ = 漣 1. Ici, la ligne de faîte passant par z ⁰ est l’axe réel, et la ligne de thalweg est la branche L de l’hyperbole 1 漣 x ² + y ²/3 = 0 telle que x 麗 0 (cf. figure). Ce chemin satisfait aux conditions (A) et on peut ici prendre exactement la ligne de thalweg comme nouveau chemin d’intégration sans changer la valeur de l’intégrale. Remplaçant alors L au voisinage du col z ⁰ = 漣 1 par le segment tangent u漣 1 + iu , 漣 r 諒 u 諒 + r , et h (face=F0019 漣 1 + iu ) par les deux premiers termes de son développement de Taylor 漣 2/3 漣 u ², on obtient l’intégrale:

La formule de Laplace, appliquée à chacun des deux intervalles [ 漣 r , 0] et [0, r ] donne:

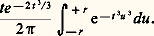
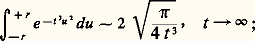d’où finalement:

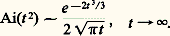6. Cas des solutions d’équations le champ réel et le champ complexe.

Systèmes dans le champ réel

Plaçons-nous d’abord dans le cas d’un système linéaire à cœfficients constants:

où A est une matrice carrée d’ordre n à coefficients complexes et x : t 料 x (t ) une fonction de classe 暈¹ sur [0, + 秊 [ à valeurs dans Cⁿ . Pour toute condition initiale a 捻 Cⁿ , l’unique solution du problème de Cauchy x (0) = a est donnée par: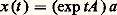

(cf. équations DIFFÉRENTIELLES). Lorsque A est diagonalisable, de valeurs propres¹ ....,^r , le comportement asymptotique de x (t ) est gouverné par la valeur propre de plus grande partie réelle. En particulier, les solutions tendent vers 0 à l’infini si et seulement si, pour tout j , on a Re^j 諒 0. Lorsque A n’est pas diagonalisable et que^j est d’indice n ^j , il existe des solutions se comportant comme t ^k e ^{j t} , où 0 諒 k 諒 n ^j 漣 1. Les solutions tendent encore vers 0 à l’infini si et seulement si Re^j 麗 0.

Examinons maintenant l’effet d’une perturbation t 料 R (t ) de A sur le comportement asymptotique d’une solution du système linéaire (1). On peut conjecturer que , si la perturbation est assez petite à l’infini, ce comportement n’est pas notablement modifié. Plus précisément, supposons A diagonalisable et soit une valeur propre de A . Si l’intégrale:

est convergente, alors, pour tout vecteur propre b de A associé à la valeur propre, il existe une solution x et une seule de l’équation perturbée:

telle que x (t ) 黎 e size=1^凞t au voisinage de + 秊.

Par exemple, soit l’équation de Bessel réduite (cf. fonctions de BESSEL, pour ce qui suit):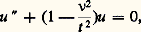

qui équivaut au système linéaire:

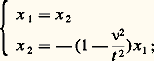ici: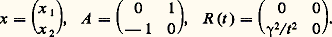

Les fonctions t 料 e ^it , et t 料 e ^-it constituent une base de l’espace vectoriel des solutions de l’équation non perturbée u + u = 0. D’après le résultat précédent, il existe donc un couple (u ¹, u ²) de solutions et un seul de l’équation perturbée tel que:

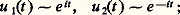cette méthode donne donc le comportement asymptotique des fonctions de Bessel.

Si, maintenant, A n’est pas diagonalisable, il convient d’imposer à R des conditions plus strictes. Lorsque^j est d’indice n ^j , on suppose que:

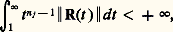ce qui entraîne l’existence d’une solution x telle que:

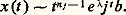Pour le comportement asymptotique des systèmes linéaires à cœfficients périodiques (par exemple, le théorème de l’équation séculaire des planètes), on se reportera à l’article équations DIFFÉRENTIELLES, La théorie de Floquet .

Le champ complexe

Pour obtenir des développements asymptotiques des solutions d’un système différentiel dans le champ complexe, l’idée principale consiste à obtenir des représentations intégrales des solutions. On utilise ensuite des développements tayloriens ou on applique à ces intégrales les méthodes esquissées au chapitre 5.

Considérons, par exemple, une équation différentielle linéaire d’ordre n :

où a ⁰, a ¹ ..., a ⁿ sont des polynômes.

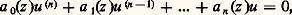Pour obtenir des représentations intégrales des solutions, les méthodes sont très variées. Citons, par exemple, la méthode de Laplace, qui s’applique lorsque les polynômes a ^j sont de degré 諒 1: on cherche les solutions sous la forme:

où L est un contour du plan complexe convenablement choisi.

Ainsi, dans le cas de l’équation différentielle:

on trouve v (z ) = exp(face=F0019 漣 﨣³/3) et:

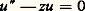
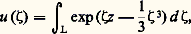où L est le contour décrit dans l’intégrale d’Airy (cf. La méthode du col , in chap. 5). Le comportement asymptotique de la solution s’en déduit.

On utilise aussi la méthode d’Euler, où:

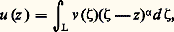pour un choix convenable de 見 et L. Une variante est la méthode de Mellin, où:

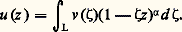Nous nous bornerons à deux exemples significatifs, importants pour les applications.

L’équation hypergéométrique

Considérons l’équation de Riemann (cf. Les équations différentielles de la physique mathématique , in chap. 2 de équations DIFFÉRENTIELLES), admettant trois points singuliers deux à deux distincts. Par une transformation homographique, cette équation se ramène à l’équation hypergéométrique:

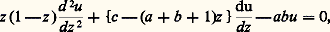où a , b , c sont des nombres complexes. Lorsque c n’est pas un entier négatif, on obtient une solution holomorphe dans le disque |z | 麗 1 par la série entière, dite hypergéométrique:

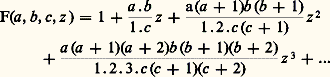qui s’écrit aussi:

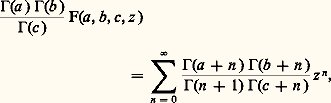où 臨 désigne la fonction gamma d’Euler (cf. fonction GAMMA).

On peut prolonger analytiquement F(a , b , c , z ) au plan fendu C 漣 R⁺ par la représentation intégrale de Mellin-Barnes:

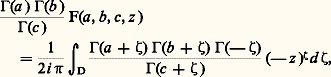où D désigne l’axe imaginaire et (face=F0019 漣 z ) size=1^﨣 = exp ( 﨣 ln (face=F0019 漣 z ) en prenant la détermination principale du logarithme, c’est-à-dire |arg(face=F0019 漣 z )| 麗 神.

Cette représentation intégrale permet alors d’obtenir la relation suivante:

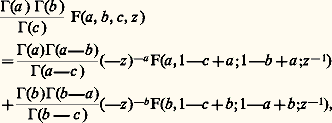qui fournit aussitôt le développement asymptotique de F(a , b , c , z ) au voisinage de l’infini sur C 漣 R⁺ (cf. équations DIFFÉRENTIELLES).

L’équation hypergéométrique confluente

L’équation hypergéométrique confluente est le cas où deux des trois singularités de l’équation de Riemann (cf. équations DIFFÉRENTIELLES) confluent en un même point. Ici encore, on se ramène au cas où ce point est à l’infini et où l’autre singularité est au point 0. On obtient alors l’équation de Whittaker, qui s’écrit:

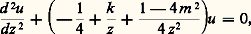où k et m sont des nombres complexes. La méthode de Laplace ou celle de Mellin fournissent une solution de la forme:

sous condition que Re(k 漣 ½ 漣 m ) 諒 0, qui est holomorphe dans le plan fendu C 漣 R^-. Cette fonction est appelée fonction de Whittaker. En développant: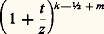

en série de Taylor, on obtient le développement asymptotique de W^k ,^m au voisinage de l’infini sur C 漣 R^-.

De nombreuses fonctions classiques apparaissent comme des cas particuliers des fonctions de Whittaker. Ainsi, la fonction d’erreur:

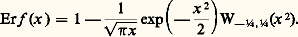Il en est de même pour le logarithme intégral. Enfin, l’équation de Bessel réduite:

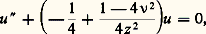est satisfaite par W⁰,ⁿ (z ) et W⁰,ⁿ (face=F0019 漣 z ). La décomposition de la fonction de Bessel J size=1^益 dans cette base (cf. fonctions de BESSEL) s’écrit:

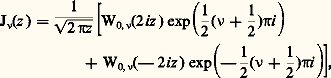ce qui fournit un développement de J size=1^益 à toute précision.

Encyclopédie Universelle. 2012.